Оптимизация дизайна сэндвич-панелей

Оптимизация композитной пластины имеет решающее значение для компоновки систем, начиная от самолетов и заканчивая гражданскими инженерными сооружениями. Хлопоты по оптимизации конструкции, представляющие интерес в настоящее время, - это минимизация функции нагрузки для сэндвич-композитной пластины. это задача оптимизации дизайна, которая оптимизирует толщину сэндвич-слоев для придания минимального веса. Дополнительный интерес для современников представляют работы по оптимизации компоновки композитных сэндвич-плит, при которых толщина наружных слоев и сердцевина берутся из-за конструктивных переменных.

ТЕОРИЯ СЭНДВИЧА Типичная сэндвич-структура соединений из трех слоев. Внешние слои изготовлены из материала, который имеет высокую прочность (армированные волокном слоистые материалы), который может передавать осевые силы и изгибающие моменты, в то время как ядро изготовлено из легких материалов, таких как пена, древесина ольхи и т. Д. Материал, используемый в сэндвич-сердечник, должен быть устойчивым к сжатию и способным передавать сдвиг. Тонкие покровные листы, т.е. слои 1 и 3, имеют толщину h1 для нижней кожи и h3 для верхней кожи. Толщина сердечника составляет h2 (рис. 1). В общем случае h1 не обязательно должен быть равен h3, но в наиболее важном практическом случае симметричных бутербродов h1 = h3.

Большинство сэндвич-структур могут быть смоделирован и проанализированы с использованием теории сдвиговой деформации для ламинатных пластин.

Для результантов N и M интегрирование осуществляется только по листам, а для поперечной силы сдвига над ядром. Конститутивные уравнения для бутерброда записываются в виде гиперматрицы, где N, M, V являются векторами нормальных сил,

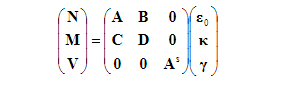
изгибающие моменты и поперечные силы сдвига, соответственно и γκε,,0 являются векторами деформаций средней плоскости, кривизны и поперечных деформаций сдвига соответственно. Коэффициенты жесткости рассчитываются как где E_i^s_j — поперечный модуль сдвига ядра.

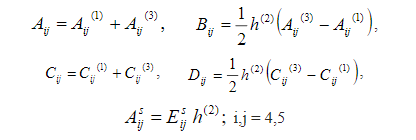
Большинство сэндвич-конструкций могут бытьсмоделировал и проанализировал с помощьютеория сдвиговой деформации дляламинат [1-3].Для результиентовNиMинтеграция осуществляется только по листам и дляипоперечная сила сдвига над ядром. Конститутивное уравнениеS для бутерброда написаны вформа гиперматриксCkEA000DC0BAВMNs0Большинство сэндвич-конструкций могут бытьсмоделировал и проанализировал с помощьютеория сдвиговой деформации дляламинат [1-3].Для результиентовNиMинтеграция осуществляется только по листам и дляипоперечная сила сдвига над ядром. Конститутивное уравнениеS для бутерброда написаны вформа гиперматриксCkEA000DC0BAВMNs0Большинство сэндвич-конструкций могут бытьсмоделировал и проанализировал с помощьютеория сдвиговой деформации дляламинат [1-3].Для результиентовNиMинтеграция осуществляется только по листам и дляипоперечная сила сдвига над ядром. Конститутивное уравнениеS для бутерброда написаны вформа гиперматриксCkEA000DC0BAВMNs0Most sandwich structures can beсмоделировал и проанализировал с помощьютеория сдвиговой деформации дляламинат [1-3].Для результиентовNиMинтеграция осуществляется только по листам и дляипоперечная сила сдвига над ядром. Конститутивное уравнениеS для бутерброда написаны вформа гиперматриксCkEA000DC0BAВMNs0

Большинство сэндвич-конструкций могут бытьсмоделировал и проанализировал с помощьютеория сдвиговой деформации дляламинат [1-3].Для результиентовNиMинтеграция осуществляется только по листам и дляипоперечная сила сдвига над ядром. Конститутивное уравнениеS для бутерброда написаны вформа гиперматриксCkEA000DC0BAВMNs0

Большинство сэндвич-конструкций могут бытьсмоделировал и проанализировал с помощьютеория сдвиговой деформации дляламинат [1-3].Для результиентовNиMинтеграция осуществляется только по листам и дляипоперечная сила сдвига над ядром. Конститутивное уравнениеS для бутерброда написаны вформа гиперматриксCkEA000DC0BAВMNs0